Projection Onto 0 Vector
To obtain vector projection multiply scalar projection by a unit vector in the direction of the vector onto which the first vector is projected. 0 1 0 0 0 0 is a projection onto the xy-plane.
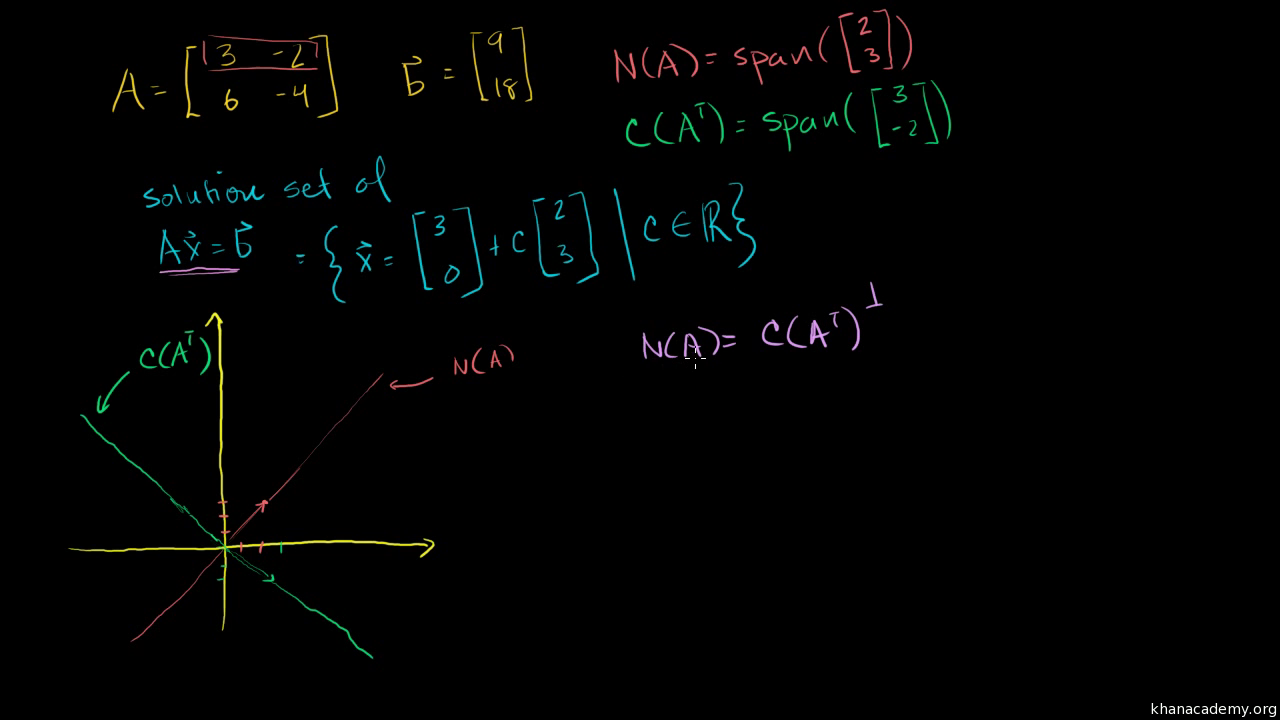
Projections Onto Subspaces Video Khan Academy
That is orthogonal to the plane from u.
Projection onto 0 vector. We know that everything in the left nullspace of A is perpendicular to. Projba a b b 2 b p r o j. V w vwcosθ.
The easiest way to do this is to first calculate the unit vector and then simply multiply it by the length of the projection of a onto b. If vis not a unit vector we know from multivariable calculus that. Free vector projection calculator - find the vector projection step-by-step.
By finding the projection of y onto span S suppose we write S v_1 v_2 v_3 where these are the vector given above. Vector projection is defined for a vector when resolved into its two components of which one is parallel to the second vector and one which is perpendicular to the second one. I Scalar and vector projection formulas.
Press the button Find vector projection and you will have a detailed step-by-step solution. We will define the vector projection formula with the help of two vectors say a and b. The idea of a vector projection in its simplest form is just the question of how much one vector goes in the direction of another.
3 If V is a line containing the unit vector v then Px vv x where is the dot product. 0 is the projection matrix onto the nullspace of AT and QQT is the projection matrix onto the column space of A. C o m p a b a b a text comp_a bfrac acdot b a comp a b a a b.
Example and are orthogonal since the dot product is 13-13300. Lets pretend that the line containing vector v is the groundLets pretend that vector u is a stick with one endpoint on the ground and one endpoint in the air. Finally we can see that the projection of any point is orthogonal to the respected projected point on vector line.
What are scalar and vector projections. In matrix form ATb Axˆ 0. ATb xa 0.
Many videos ago we introduced the idea of a projection and in that case we dealt more particularly with projections onto lines that went through the origin so if we had some line lets say L and lets say L is equal to the span of some vector V or you could say alternately you could say that L is equal to the set of all multiples of V such that the scalar factors are just any real numbers. Thus two non-zero vectors have dot product zero if and only if they are orthogonal. The projection of u.
Find the projection of vector a 1. The dot product is closely related to orthogonal projections of one vector onto the other. Y npdotx y npdoty y for the vector projection of x onto y.
0 on vector b 4. All eigenvalues of an orthogonal projection are either 0 or 1 and the corresponding matrix is a singular one unless it either maps the whole vector space onto itself to be the identity matrix or maps the vector space into zero vector to be zero matrix. This is fairly intuitive.
Since the sun is shining brightly vector u would therefore cast a shadow on the ground no. Projecting One Vector onto Another Vector Illustrated Imagine its a clear day and the sun is shining down upon the Earth. The equation of the plane 2 x y z 1 implies that 2 1 1 is a normal vector to the plane.
V W V cosO O V W W V O V W V W W cosO. As VaidAbhishek commented the above formula is for the scalar projection. That v S 2 0 2 truly is orthogonal to S is proved by noting that it is orthogonal to both v 1 and v 2.
The projection in this case would be the vector OP. Jecting onto after which we can use the fact that e is perpendicular to a1 and a2. You find the components of y along each of the v_i call these coefficients a_1 a_2 a_3 then you can write P_Sy a_1v_1 a_2v_2 a_3v_3 thus youve written the projection of y into span S.
Leaving the horizontal component. Onto a plane can be calculated by subtracting the component of u. If you project the vector 1 1 1 onto 2 1 1 the component of 1 1 1 that was erased by this projection is precisely the component lying in the plane.
From the projection of v onto S is the vector. If θ 0 then the projection vector of overlineAB will be overlineAB. The scalar projection of b onto a is the length of the segment AB shown.
P r o j b a b b a b b a b b 2 b. Minus the vertical component of u. Therefore v v S where v S 0 2 0 and.
The dot product and orthogonal projections. When we were projecting onto a line A only had one column and so this equation looked like. A 1 T b Axˆ 0 and a 2 Tb Axˆ 0.
So all we need to do is take the vector b and scale it by the scalar projection. If θ π then the projection of overlineAB will be overlineBA. The formula then can be modified as.
We have kAxbk 2 2 kAxx 0Ax 0 bk 2 Axx 0Ax 0 b T Axx 0Ax 0 b kAxx 0k 2 2 kAx 0 bk 2 2xx 0 TA Ax 0 b kAxx 0k2 2 kAx 0 bk 2 2 2xx 0TATAx 0 ATb kAxx 0k2 2 kAx 0 bk 2 2 A TAx 0 A Tb 0 3. Two vectors are orthogonal if ab 0 a b 0. The closest point on the vector line to a point already on the vector line is just that same point.
We do not consider these trivial cases. One important use of dot products is in projections. Writing this as a matrix product shows Px AATx where A is the n 1 matrix which contains vas the column.
The vector projection is of two types. Guide - Vector projection calculator To find projection of one vector on another. Scalar projection that tells about the magnitude of vector projection and the other is the Vector projection which says about itself and represents the unit vector.
Calculate dot product of these vectors. If θ π2 or θ 3π2 then the projection of overlineAB will be a zero vector. If the vector veca is projected on vecb then Vector Projection formula is given below.
The scalar projection of one vector onto another also called the component of one vector along another is. Select the vectors dimension and the vectors form of representation. If you think of the plane as being horizontal this means computing u.
A b 1 4 4 2 0 4 4 8 0 12 Calculate the magnitude of vector b. B 4 2 2 2 4 2 16 4 16 36 6 Calculate vector projection. Note that e b Axˆ is in the nullspace of AT and so is in the left nullspace of A.
Write the vector v 2 2 2 as the sum of a vector in S and a vector orthogonal to S. Type the coordinates of the vectors. This idea is geometrically represented by the figure below with vector a being projected onto vector b.
So b proj.

Scalar And Vector Projections Kristakingmath Youtube
Scalar And Vector Projections Kristakingmath Youtube

Scalar Projection Vector Projection By Solomon Xie Linear Algebra Basics Medium

Projection Of A Vector On A Line Angle Between Two Vectors Videos Q A
Projections Onto Subspaces Video Khan Academy

Another Example Of A Projection Matrix Video Khan Academy
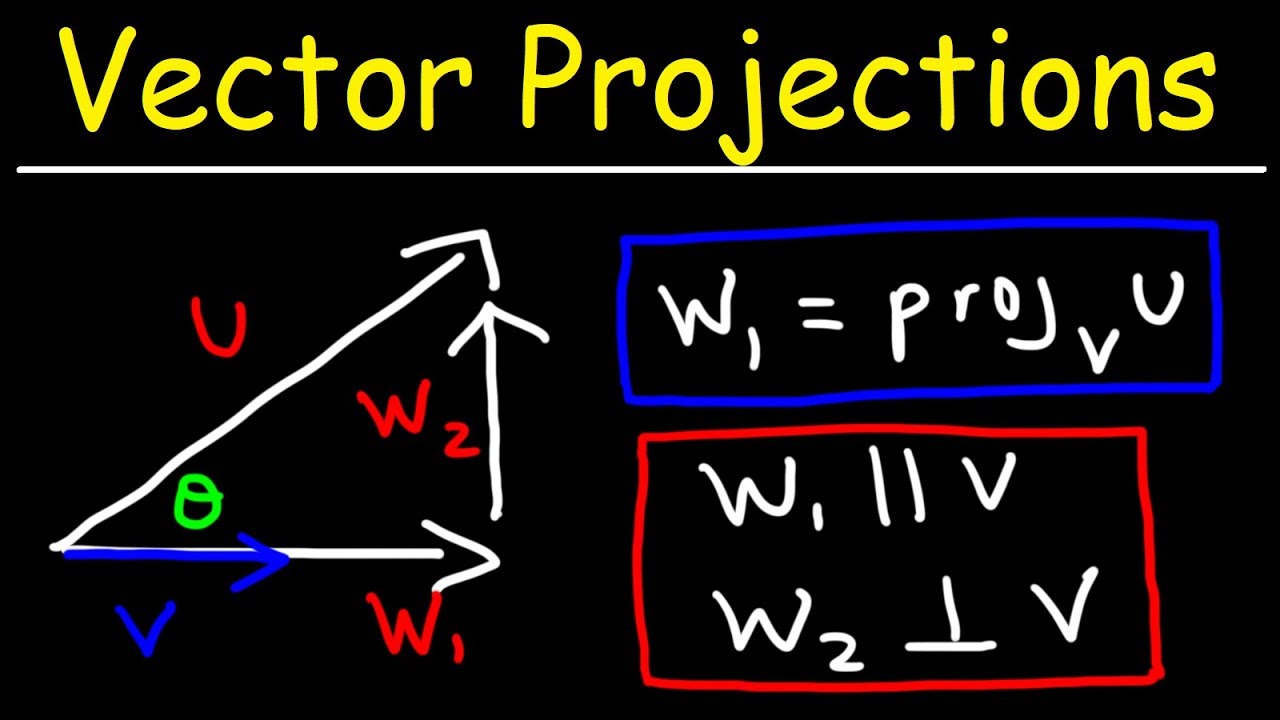
Calculus 3 Vector Projections Orthogonal Components Youtube

Why Is It Called Orthogonal Projection Why Not Just Projection Mathematics Stack Exchange

Vector Projections Dr Shildneck Ppt Download

Ex 10 3 3 Find Projection Of Vector I J On Vector I J
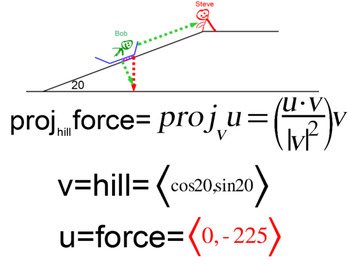
Vector Projection Of U Onto V Intro 4 Assignments For Power Point


Posting Komentar untuk "Projection Onto 0 Vector"