Projection Matrix Eigenvalues 0 1
And for any such matrix A. Ak 0 for some specific k.

Hessian Matrix And Quadratic Approximation With Example In Python Quadratics Partial Derivative Matrix
Then the usual 3 steps.

Projection matrix eigenvalues 0 1. In other words for a 2 2 Hermitian matrix to have a single degenerate eigenvalue it must be a diagonal matrix with the two diagonal entries equal a multiple of the identity matrix. The eigenvectors for λ 0which means Px 0xfill up the nullspace. P is singularso D 0 is an eigenvalue.
2 Symmetric and orthogonal matrices. X 0 1 is an eigenvector with eigenvalue λ 0. Eigenvectors corre-sponding to eigenvalue 1 ll the subspace that P projects onto.
Write u0 as a linear combination of the eigenvectors. It describes the influence each response value has on each fitted value. In general the corresponding eigenspaces are respectively the kernel and range of the projection.
All eigenvalues of an orthogonal projection are either 0 or 1 and the corresponding matrix is a singular one unless it either maps the whole vector space onto itself to be the identity matrix or maps the vector space into zero vector to be zero matrix. The diagonal elements of the projection matrix are the leverages which describe the influence each response value has. The nullspace is projected to zero.
A 0 1 0 0 0 0 1 So. In statistics the projection matrix displaystyle sometimes also called the influence matrix or hat matrix displaystyle maps the vector of response values to the vector of fitted values. Let A be an nxn matrix and let λ be an eigenvalue of A with corresponding eigenvector v.
A λ 0 0 λ 20. A Find the resolvent of A. If 0 is an eigenvalue then the nullspace is non-trivial and the matrix.
This implies that an orthogonal projection is always a positive semi-definite matrix. If P is a projection matrix then it has two eigenvalues. 0 1 1 Ae3 1 0 1 Relative to this basis the matrix of A is A 1 0 1 2 1 0 3 1 1 If we change to a different basis say x1 1 1 1 x2 1 1 0 x3 1 1 2 then the matrix Achanges.
An nxn matrix A is called idempotent if A 2 A. We can use its trace or the fact that its a projection matrix to find that P has the eigenvalue 1. If all eigenvalues are zero then that is a Nilpotent Matrix.
A projection matrix has eigenvalues 1 and 0. We do not consider trivial cases of zero matrix and identity one. The only eigenvalues of a projection matrix are 0and 1.
A 1 A 1 Eigenvector equation for a symmetric matrix Au k ku k which can be written as AU DU or A DU 0 where D is a diagonal matrix whose elements are eigenvalues D 2 6 4 1. Let us start with a simple case when the orthogonal projection is onto a line. Hence solving λλ 1 0 the possible values for λ is either 0 or 1.
B Prove that P has r rankP LI eigenvectors in CP and n-r LI eigenvectors in NP. Adds to 1so D 1 is an eigenvalue. Each column of P adds to 1 so λ 1 is an eigenvalue.
The eigenvalues are 0 and 1. C Deduce that P is diagonalizable. Multiplication with A is projection onto the x-axis.
Geometrically zero eigenvalue means no information in an axis. Projection and the eigenvalue of 0 corresponds to vectors perpendicular to the line of projection. A 1 0 1 1 0 So.
The eigenvalues of P are 0 0 and 1. If b is perpendicular to the column space then its in the left nullspace NAT of A and Pb 0. Let Pe MnR be a projection matrix ie.
Consider the polynomial pxx 2. So if one or more eigenvalues are zero then the determinant is zero and that is a singular matrix. The inverse is also symmetric.
P is symmetric so its eigenvectors 11 and 11 are perpendicular. 0 and 1 we will assume P 0 and P I for simplicity. P is singular so λ 0 is an eigenvalue.
Here x 2 1. What does it mean if a matrix has an eigenvalue of 0. Thus the idempotent matrix A only have eigenvalues 0 or 1.
Note that A and QAQ 1 always have the same eigenvalues and the same characteristic polynomial. Projection matrices and least squares Projections Last lecture we learned that P AAT A 1 AT is the matrix that projects a vector b onto the space spanned by the columns of A. Each eigenvalue of an idempotent matrix is either 0 or 1.
The eigenvectors for D 0 which means Px D 0x fill up the nullspace. To even further reduce the computational burden of the random projection method at a slight loss in accuracy the random projection matrix R may be simplified by thresholding its values to 1 and 1 or by matrices whose rows have a fixed number of. Comparing these two computations we obtain.
Is an eigenvector with eigenvalue λ 1. Here x 1 11. Indeed we know that for a projector P defined on a vector space E we have E ker Poplus operatornameimPker Poplus kerI-P ker P is the eigenspace associated with the eigenvalue 0 kerI- P the eigenspace associated with the eigenvalue 1.
A x y x 0 ie. A Prove that I 0 or 1 1 are the only possible eigenvalues of P. Only 0 or 1 can be an eigenvalue of a projection.
X 1 0 is an eigenvector with eigenvalue λ 1. U0 3 1T. M 3 7 5 and U is matrix whose columns are eigenvectors u k 922.
The eigenvectors for D 1 which means Px D x fill up the column space. The only eigenvalues of a projection matrix are 0 and 1. All eigenvalues of an orthogonal projection are either 0 or 1 and the corresponding matrix is a singular one unless it either maps the whole vector space onto itself to be the identity matrix.
Useyour geometricunderstandingtofind the eigenvectors and eigenvalues of A 1 0 0 0. For this example since x1 e1e2e3 x2 e1e2 and x3 e1 e2 2e3 we can compute Ax1 Ae1 e2 e3 Ae1 Ae2 Ae3 2 3 3 a1. Decomposition of a vector space into direct sums is not unique.
Theorem 2 The matrix A is diagonalisable if and only if its minimal polynomial has no repeated roots. Eigenvectors corresponding to eigvenvalue 0 ll the perpendicular subspace. The matrix A projects vectors onto the line through the origin that makes an angle of theta degrees with the positive x-axis in number 1 above the line was yx ie theta was 45 degrees from the positive x-axis.
Then by definition of eigenvalue and eigenvector Av λ v. A matrix A is diagonalisable if there is an invertible matrix Q such that QAQ 1 is diagonal. P is symmetric so its eigenvectors 11 and 1.
Final Exam Problems and Solution. The resolvent of a matrix Ais the inverse of that thing A λI whose determinant we set to zero. Every nonzero vector in the column space of P that is in the projection plane is an eigenvector corresponding to the eigenvalue 1.
Since P has rank 1 we know it has a repeated eigenvalue of 0. PT P and P2 P. If b is in the column space then b Ax for some x and Pb b.
Since x is a nonzero vector because x is an eigenvector we must have.

Could We Get Different Solutions For Eigenvectors From A Matrix Stack Overflow

Ex 3 4 17 Find Inverse 2 0 1 5 1 0 0 1 3 Ncert Ex 3 4

Linear Algebra X App Is Now Available On The App Store Linearalgebrax Linearalgebra Math App Rules Theorems Properties Algebra Linear Equations Theorems

Solved Let A Be The 6 6 Symmetric Matrix Defined As Chegg Com

Gauss Seidel Method The Algorithm And Python Code

Monte Carlo Integration Both The Explanation And The Python Code Monte Carlo Method Coding Uniform Distribution
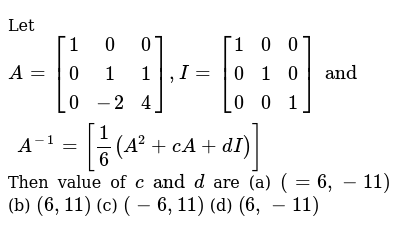
Let A 1 0 0 0 1 1 0 2 4 I 1 0 0 0 1 0 0 0 1 And A 1 1 6 A 2 Ca Di Then Value Of C And D Are A 6 11 B 6 11 C 6 11 D 6 11

Proof Eigenvalue Is 1 Or 0 If A Is Idempotent Youtube

Understanding Basics Of Measurements In Quantum Computation Quantum Computer Quantum Quantum Mechanics

Forward Substitution The Algorithm And The Python Code Coding Algorithm Linear Equations

Pdf On The Determinant Of 0 1 Matrices
Posting Komentar untuk "Projection Matrix Eigenvalues 0 1"