Projection Using Dot Product

So and w 1. The scalar projection of b onto a is the length of the segment AB shown in the figure below.

Converting A Carbohydrate Fischer Projection To A Haworth And Chair Resume Template Infographic Chemistry

The dot product can also help us measure the angle formed by a pair of vectors and the position of a vector relative to the coordinate axes.

Projection using dot product. It even provides a simple test to determine whether two vectors meet at a right angle. Properties of the Dot Product Let x y z be vectors in R n and let c be a scalar. 31 25.

Using Properties of Dot Products Let and Find each dot product. Point projection on Bézier curves can be easily accomplished using Newton Iteration to try to minimize the dot product between the vector connecting the point P and its projection on curve C and the curve tangent vector C at the same parameter. I Scalar and vector projection formulas.

You can do arithmetic with dot products mostly as usual as long as you remember you can only dot two vectors together and that the result is a scalar. The dot product follows the distributive law also ie. I Dot product in vector components.

Two vectors are orthogonal if the angle between them is 90 degrees. One important use of dot products is in projections. That is the vector dot product can be used to find projection of a vector on a line.

Compute the dot product of the following vectors. I assume you are referring to the shortest distance between a point in mathbb R3 and a plane. Is a scalar multiple of Take dot product of each side with and are orthogonal.

When the dot product is zero we have a. Projections and components Projections. V w vw cosθ.

I Dot product in vector components. In finding the component in parallel to one vector the vector is projected on to another. It is often called the inner product or rarely projection product of Euclidean space even though it is not the only inner product that can be defined on Euclidean space see Inner product space for more.

I Properties of the dot product. In Euclidean geometry the dot product of the Cartesian coordinates of two vectors is widely used. The dot product essentially tells us how much of the force vector is applied in the direction of the motion vector.

O W V v cosθ v w w. We can derive the calculation of length of vector p b as well as the vector itself. Solution Begin by finding the dot product of and a.

Aa aa cos 0 a 2 Property 5. The dot product can used to calculate the projection of one vector onto another vector. Notes on the dot product and orthogonal projection An important tool for working with vectors in Rn and in abstract vector spaces is the dot product or more generally the inner product.

V w vwcosθ. Whenever they dont coincide the inner product is used instead of the dot product in the formal definitions of projection and rejection. I Properties of the dot product.

This is given by the orthogonal projection of a line into another line ie projecting a line from the origin into the plane into the normal vector of the plane. For a three-dimensional inner product space the notions of projection of a vector onto another and rejection of a vector from another can be generalized to the notions of projection of a vector onto a plane and rejection of a vector from a plane. The dot product is closely related to orthogonal projections of one vector onto the other.

I Scalar and vector projection formulas. I Dot product and orthogonal projections. The vector projection of b onto a is the vector with this length that begins at the point A points in the same direction or opposite direction if.

Lets come to the interesting use case. The dot product gives us a very nice method for determining if two vectors are perpendicular and it will give another method for determining when two vectors are parallel. The dot product and orthogonal projections.

Note as well that often we will use the term orthogonal in place of perpendicular. Thus using we see that the dot product of two orthogonal vectors is zero. The dot product is closely related to orthogonal projections of one vector onto the other.

Before moving to projections lets do some examples to get more familiar with the dot product. Vector dot product is understood as product between components in parallel to each other. V W V cosO O V W W V O V W.

Projection you can use the dot product as follows. Conceptually we are looking at the shadow of one vector projected onto another sort of like in the case of a sundial. The dot product and orthogonal projections.

The algebraic definition of the dot product in Rn is quite simple. The vector p b is the projection of vector b onto vector a. Answer 1 of 3.

We just used projections and so indirectly the dot product to calculate the shortest distance from P to L. Thanks to A2A An important use of the dot product is to test whether or not two vectors are orthogonal. Just multiply corresponding components and add.

Now if two vectors are orthogonal then we know that the angle between them is 90 degrees. The dot product of a vector to itself is the magnitude squared of the vector ie. One of the major uses of the dot product is to let us project one vector in the direction of another.

Ab c ab ac. In the figure a a is the projection of q q onto p p That means a a can be calculated using vector dot product. I Dot product and orthogonal projections.

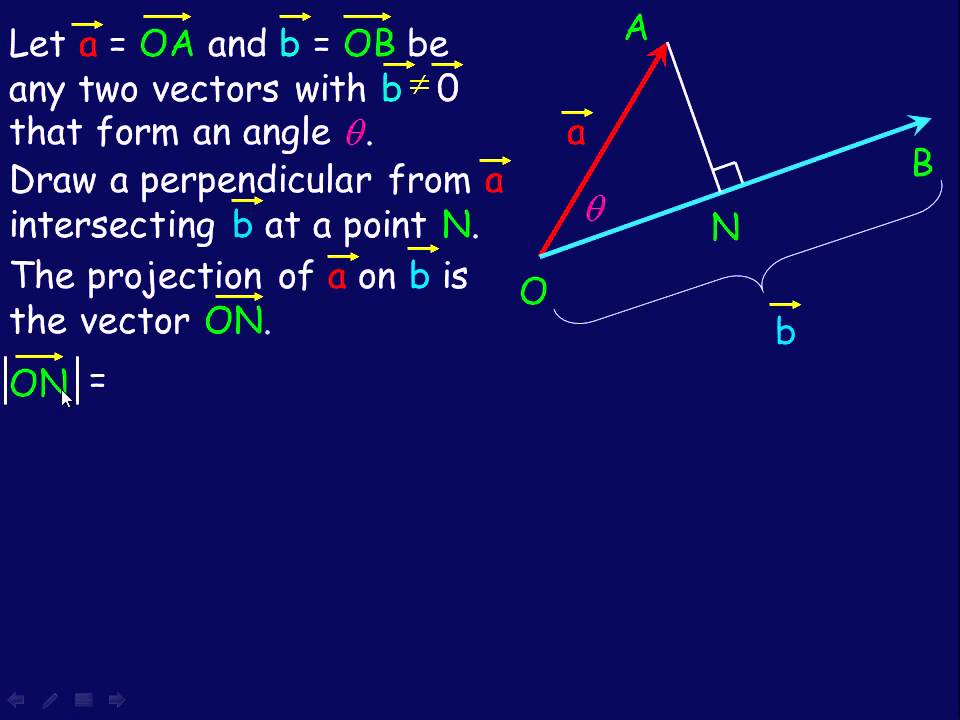
Applications Of The Dot Product Avi Calculus 12th Maths Mathematics

Cosines Learning Mathematics Math Formulas Mathematics

File Scalar Product Dot Product Svg Physics And Mathematics Free Math Resources Mathematics

Zaitsev S Rule Regioselectivity Of E2 Elimination Reactions Practice Problems Chemistry Lessons Reactions Organic Synthesis

Projection Of Force In Statics Examples Of Force Engineering Courses Engineering Student

File Scalar Product Dot Product Svg Physics And Mathematics Free Math Resources Mathematics

Calculus Iii The Dot Product Level 8 Scalar Vector And Orthogonal Projections Calculus Dots Absolute Value

Dot Product Explained Basic Physics Physics 12th Maths

Vector Product Vector Calculus Calculus Physics And Mathematics

Converting Fischer Projection To Bond Line Structure Using The R And S And Swap Method Organic Chemistry Study Organic Chemistry Chemistry Classroom

Pin On Einhorn Tapete

Cross Product Components Math Methods Teaching Math Algebra

Projection Of Force In Statics Examples Of Force Engineering Courses Engineering Student

Dot Product As Projection Of Vectors Physics And Mathematics Learn Physics Math Vector